Checksums and Bugs

Bugs Are a Joke

Those familiar with the history of computers know all too well that bugs are a joke. Literally. Like "Walt Disney on Ice" literally. The first well known defect (the term we use professionally to describe a bug, or "undesired/unexpected behavior") was a moth. That's right - not a typo. You see, back in the days of Shannon (remember him?), computers had a lot of moving parts. And sometimes, bugs would fly into the moving parts. And sometimes the bug might have an unfortunate experience with the moving parts. True story - a moth flew into a relay back in 1946 and Grace Hopper found the moth (essentially finding the first "bug"). Incidentally, Grace Hopper is totally awesome and was a true pioneer in the field of computer science.

Checksums

A checksum is a fancy term we use for making sure computers didn't miss something. Not surprisingly, checksums are used in Information Theory (again, remember Shannon?). Bugs notwithstanding, the computer world is not perfect. Stuff happens, and that stuff can be out of our control. Signals are susceptible to interference. In the computer world, all communication boils down to 1's and 0's. But nature doesn't always play nicely and sometimes all those pretty copper or fiber lines that carry your Internet signals get mixed signals. If too many mixed signals go unnoticed, bad things tend to happen. Happily, pioneers of Information Theory understood this (keep in mind that this dates back to WWII, where radio communication was expensive but extremely important). They came up with the notion of a checksum. There are a ton of really good uses, but this is a trivial example:

For every 7 bits I send, I will add an 8th bit which will make the number of 1's in the 8 bit string even; when you receive my message, you can check that the number of 1's is even.

Example:

I send the 7 bit value:

0110011

There are 4 1's in the string - an even number; consequently, I do NOT need to add another 1, so I add a 0 instead.

01100110

Now, when you receive the value, you will remove the last 0 from the byte (a byte is 8 bits), resulting in the original message:

0110011

You will count the number of 1's, see that there are 4 - which is even!.

But what happens when something goes awry during the transmission? Let's take a look. I send the original message (with the "0" appended):

01100110

But because of transmission errors, you receive:

01000110

You count the number of 1's in the message and see that the value is odd, not even. You have just detected an error (because of checksums)! All that you can deduce is that there was an error in the transmission - you do not know where the error occurred - just that there is an error.

This is a simple example, but hopefully you get the gist of checksums. Be aware that the particular example I illustrated will only detect one error. Multiple errors may go undetected. Fear not - science has provided more complex checksum methods to account for that; as well, some methods can offer error correction. That is to say that not only can errors be detected, but in some cases, the errors can be corrected - wild!

OK, But What About The Real World?

Great question! You see checksums all the time. UPC symbols have them - so any time you buy something that is scanned, you are seeing checksums at play (technically it is a check digit, but the concept is the same).

Checksums are also used in ISBN numbers. If you are old enough to remember what a real book looked like, you might recall that each book has its own ISBN. Boring, but it might help on Final Jeopardy.

Try It At Home

Need a weekend project? Try this on for size: credit card authorization did not used to happen instantly. Merchants would batch up all the transactions over a set amount of time and then process them with the credit card company. And sometimes the processing used unreliable communication links (sound familiar yet?). In order to help identify which credit card numbers were transmitted in error, credit cards has a checksum built in. This is still used today. Take your favorite credit card and do the following:

1. Multiply the first number by 1
2. Multiply the second number by 2
3. Multiply the third number by 1
4. Multiply the fourth number by 2
5. ...
6. Repeat for all numbers except for the last number
7. Sum up all the products
8. Add the last number to the sum of the products
9. If the total sum is evenly divisible by 10 (modulo 10 if you are mathy), the number is valid

For example, give the 16 digit credit card number and the multiplier:

  1234 1234 1234 123?

x 1212 1212 1212 121 

We get the sum:

      1438 1438 1438 143 = 56

The check digit needs to be a value such that when added to 56, will be divisible by 10. We need a 4. The complete credit card number is then:

1234 1234 1234 1234

And How Does This Relate To Bugs?

Fair question. This is where the boring part comes into play, but it is important to understand. Remember when I was talking about motion detection? When I was writing the detection algorithm, I noticed that the edges of the image did not look quite right. When I looked into it a bit further, I found that the image was being improperly handled: my algorithm was cropping part of the image (to focus on the section of the image which I was interested in), but the code I used to crop the image was not properly handling decompression/compression. As a consequence, parts of the compressed image that was cropped off still had some data within the image. Think about it like this:

The compressed image has localized data; basically a count of the number of pixels of each color within a quadrant of the image, along with a checksum of the value. But when I remove part of the image, the count was not updated and the checksum does not validate.

By way of example, let me illustrate. Remember this dude?

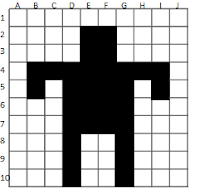The Guy

If we want to compress the image, we might break up the image into quadrants like this:

Quadrants

Now, count the number of black squares in each quadrant and add a check digit that value. For each of the top two quadrants, we have 11 full black squares. In the lower quadrants, we have 7 black squares. Checksum modulo 10 and our values for the top quadrants are 11 and 9 (11 is the count, 9 is the check digit) and the lower quadrants are 7 and 3. We can represent the values as touples, and they look like this: (11, 9) and (7, 3).

Lets say that I crop the image, like so:

Cropped for profile pic

But whoops! I did not update the compression data with checksums! The top two quadrants will still validate (11 ,9), but the two lower quadrants are in error. The lower quadrants should be (4, 6) but are still (7, 3). By virtue of not recalculating the compression values, the data we have about the image describes part of the image which is no longer present.

Is This A Problem?

No, not at all. This does not affect how we perceive the image - the image will continue to look as it should because the compression error has no visual manifestation. But software that looks at the checksum will notice that something does not quite add up (pun intended).

Endgame

What is the takeaway? Hopefully you have a slightly better understanding of what a checksum is and how it works. Additionally, you now have an anecdote to tell the next time someone says that they found a bug in some software.

Also, for the purpose of this post, I use the term "checksum" to be interchangeable with the term "check digit". While the two terms are related, they are not exactly the same. Checksums are typically more complex than what I describe, but the concept is the same. But checksums are more widely known, so we'll stick with that term.